푸리에 변환 3

어느새 3편이다. 이번 글에서는 Online FFT에 대해 집중적으로 다루고 싶다. 사실 그 전에 cubelover님의 블로그를 읽다가 XOR convolution을 FFT로 하는 방법에 대해 알게 되었는데, 이 부분을 조금 알고 넘어가면 좋을 것 같아 짧게 다뤄보도록 하겠다.

XOR Convolution

나중에 쓸게요

Online FFT

일반적으로 FFT는 합성곱을 빠르게 계산함으로써 효율적으로 문제를 해결할 수 있다는 장점을 가지고 있다. 즉, 다음 문제를 빠르게 해결할 수 있는 것이다.

Given $A=\lbrace a_0,a_1,\cdots,a_n\rbrace, B=\lbrace b_0,b_1,\cdots,b_n\rbrace$, Find $C=\lbrace c_0,c_1,\cdots,c_n \rbrace, c_i=\sum_{i+j=k}a_i\times b_j$

이제는 FFT를 활용하여 이와는 조금 다른 결의 문제를 해결해보고자 한다.

Given $a_i,b_i$ sequentially, Find $c_i=\sum_{i+j=k}a_i\times b_j$

즉, 기존에는 합성곱을 계산하는 배열이 완전히 주어졌지만, 새로운 문제의 경우에는 값들이 순차적으로 주어지게 되어 짝수항과 홀수항으로 나눠서 계산하는 Cooley-Tukey FFT 알고리즘을 사용할 수 없는 것이다.

Block Decomposition

jinhan814님의 블로그와 Kiri8128님의 블로그 를 정말 많이 참고하였다!

합성곱을 구하는 과정을 그림을 통해 살펴보자.

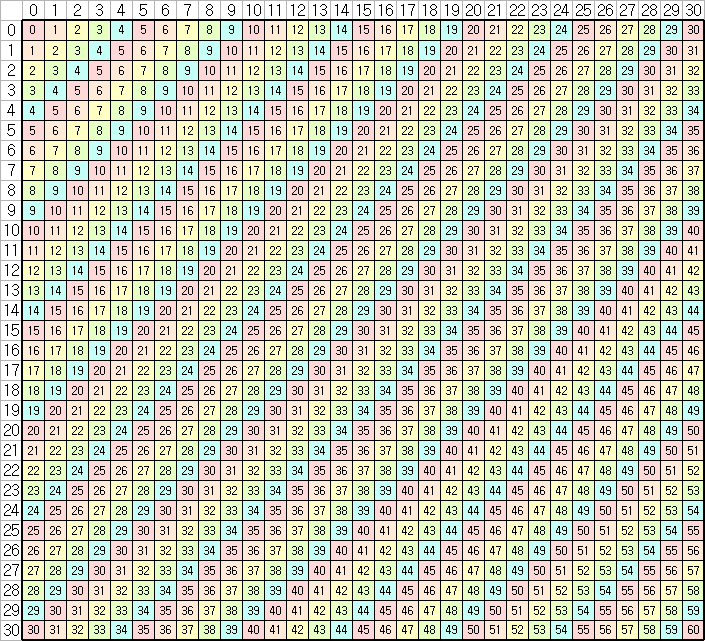
다음과 같은 그리드에서 $a_i+b_j$가 $(i,j)$번째 칸에 저장되어 있다고 해보자. 그렇다면 합성곱의 결과 $c_k$에 관여하는 칸들은 $i+j=k$, 즉 같은 색으로 칠해진 대각선 위에 존재하는 칸들이 $c_k$에 기여한다고 볼 수 있으며, FFT는 대각선의 합을 더 효율적으로 계산할 수 있도록 도와주는 알고리즘이라고 볼 수 있다. 이제 Online FFT를 위해서 저 칸들을 적절히 모아 블록으로 만들어보자.

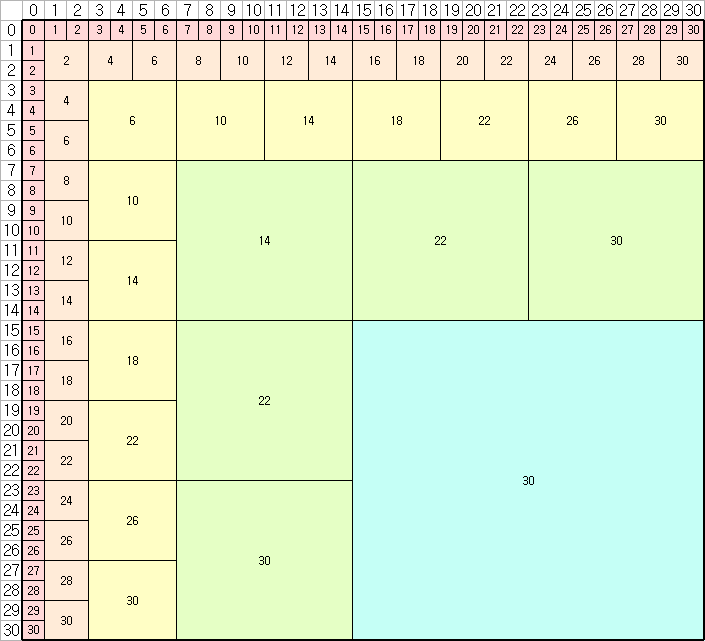
이때, 각 블록의 범위를 $[l_1,r_1],[l_2,r_2]$로, 크기를 $s=r_2-l_2=r_1-l_1$로 잡을 수 있고, 블록에 적힌 숫자는 $\max(r_1,r_2)$이다. 이후 $a_i,b_i$가 주어졌을 때, $(i,j)$ 칸이 속한 블록을 이용하여 $c_{l_1+l_2}\sim c_{r_1+r_2}$의 값들에 일종의 업데이트를 해준다고 보면 된다.

칸들을 위 블록처럼 모으는 이유는 무엇일까? 블록을 활용한 Online FFT 구현의 핵심은 $c_k$를 구할 때 $i+j=k$ 대각선에 위치한 칸들이 속한 블록들이 모두 업데이트, 즉 계산 가능해야한다는 점이다. 이 말은즉슨 $(i,j)$칸이 속한 블록의 끝범위가 $k$ 이하여야한다는 것이고, 이는 블록 안에 적힌 값이 $k$ 이하임을 의미한다. 그렇기에 다음과 같이 블록을 나누게 되면 대각선 위에 $k$보다 큰 값들이 위치하게 되므로 정상적으로 합성곱을 구할 수 없다.

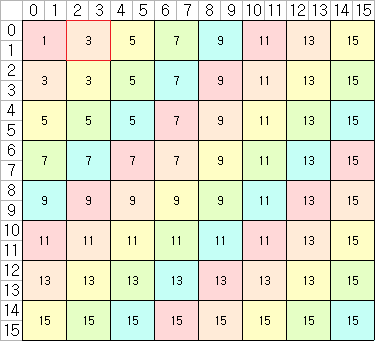
구현은 블록의 재귀적인 형상을 고려하여 규칙을 찾아낼 수 있다. 먼저 $[0,n]$을 블록들의 크기로 적당히 쪼개주면 $[0],[1,2],[3,4,5,6],[7,\cdots,14],\cdots$가 된다. 그리고 이제 어느 블록들을 업데이트 해주면 되는지 구해보자. 앞에서 설명한 것처럼 $a_i,b_i$가 주어졌을 때 $\max(r_1,r_2)=i$인 블록들을 업데이트 해주면 되겠다. 그런데, 이 블록들을 어떻게 효율적으로 순회할 수 있을까?

먼저 다음은 자명한 사실이다. $i$번째 값이 들어왔을 때 $i$가 속하는 구간의 길이는 $2^{\text{__lg}(i+1)}$이다. 그리고 하나 정말 놀라운 사실은 $i$가 구간에서 $k$번째 값일 때, 업데이트 해야할 블록들은 $(0,i)$에서 아래로 내려가면서 만나는 길이가 $2^0,2^1,\cdots,2^{\text{__builtin_ctz(k)}}$인 블록들이다. 대충 손으로 아무 $i$나 잡고 직접 $k$를 구해서 블록들을 찾아보면 이해가 쉽게 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void push(int p, int q)
{
    const int n = A.size();
    const int s = __lg(n+1);
    const int k = __builtin_ctz(n+1-((1<<s)-1));

    int x=n,y=0;
    for(int i=0;i<=k;i++)
    {
        update(x,x+(1<<i),y,y+(1<<i));
        if(x!=y) update(y,y+(1<<i),x,x+(1<<i));
        x -= 1<<i;
        y += 1<<i;
    }
}

선택된 블록들에 대해서 합성곱을 구해준 뒤, 결과를 반영해주면 된다.

1
2
3
4
5
6
7
void update(int l1, int r1, int l2, int r2)
{
    poly a(A.begin()+l1, A.begin()+r1);
    poly b(B.begin()+l2, B.begin()+r2);
    poly c = multiply(a,b);
    for(int i=0;i<c.size();i++) C[l1+l2+i] += c[i];
}

사실 위 방법으로 Bin 문제를 풀 수 있다고 하는데 많이 어려워 보인다.

• Previous
  푸리에 변환 2