미적분학의 기본정리
FTC 1
If $f$ is continuous on $\lbrack a,b \rbrack$, then the function is define by
\[F(x) := \int_{a}^{x}f(t)\ dt\]Then,
\[\frac{d}{dx} \int_{a}^{x}f(t)\ dt = f(x)\]FTC 2
\[\int_{a}^{b}f(x)\ dx = F(b)-F(a)\]FTC1은 미분과 적분이 역연산의 관계에 있음과 함수 f의 정적분으로 정의된 함수가 f의 수많은 부정적분 F 중 하나임을 증명한다.
FTC2는 정적분과 부정적분의 관계를 증명한다. 즉 주어진 함수의 원시함수와 넓이의 관계성을 증명한 것이다.
정말 아름답다 o:
증명은 쉽게 할 수 있으니 그 느낌을 이해해보려고 노력하자.
다변수함수의 연쇄법칙
- https://blog.naver.com/mindo1103/90103548178
일변수 함수에서의 연쇄법칙은 다음과 같이 적용할 수 있었다.
\[\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}\]다변수 함수의 경우에는 어떻게 적용할 수 있을까?
$u$가 $x_1,x_2,\cdots,x_n$에 대해 미분 가능한 $n$변수 함수이고, $x_i$가 각각 $t_1,t_2,\cdots,t_m$에 대해 미분 가능한 $m$변수 함수라면 $u$는 $t_1,t_2,\cdots,t_m$에 대해 미분 가능한 함수이고, 다음이 성립한다.
\[\frac{\partial u}{\partial t_i}=\frac{\partial u}{}+\frac{}{}+\cdots+\frac{}{}\]벡터장
- https://en.wikipedia.org/wiki/Vector_field
벡터장이란 벡터를 입력값과 출력값으로 가지는 함수라고 할 수 있다.
엄밀한 정의는 다음과 같다.
$\R^n$의 부분집합 $S$를 잡자. 이때, 벡터장은 벡터함수 $F : S\rightarrow \R^n$로 정의된다.
\[F(x,y,z)=P(x,y,z)\hat{i}+Q(x,y,z)\hat{j}+R(x,y,z)\hat{k}\]중적분
정적분의 개념 확장 -> 독립변수가 2개 이상! 즉 공간에서 적분을 가지고 논다. 이때, 웬만해서는 적분이 잘 되지 않기에 좌표계를 변환해준다. 보통 2차원에서는 극좌표로, 3차원에서는 구면좌표계와 원통좌표계로 변환한다. 선행 지식으로 야코비안이 필요하다.
그저 적분을 여러번하는 반복적분과는 다른 개념이다.
Repeated integral $\neq$ Multiple integral
\[\int\ \iint\ \iiint\ \oint\ \oiint\ \oiiint\]선적분
곡선에 대한 적분이다. 기존 적분이 주어진 구간 사이의 값에 대해서 적분값을 구했다면 이제는 한 차원 더 나아가서 $n$차원에서 정해지지 않은 형태의 곡선 위에 존재하는 모든 점들에 대해서 적분을 구하는 것이다. 스칼라장, 벡터장에 따라서 적분 방법이 달라진다.
스칼라장에서의 선적분
- https://freshrimpsushi.github.io/posts/line-integral-of-scalar-field/
- https://blog.naver.com/PostView.nhn?blogId=cindyvelyn&logNo=221828338012&from=search&redirect=Log&widgetTypeCall=true&directAccess=false
- https://gosamy.tistory.com/235
적분구간이 $C$라는 곡선 위고, 이들을 잘게 쪼갠 $ds$에 대해서 $f(x,y)$를 선적분하자!
즉, 아래 그림에서 커튼처럼 보이는 면적을 구하는 것이라고 할 수 있다.
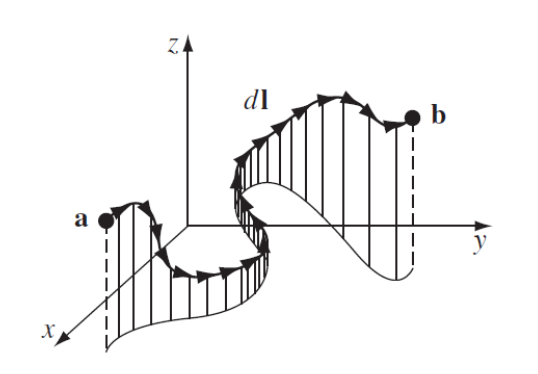
이는 매개변수 치환을 통해 풀어낼 수 있다.
고등학교 미적분에서 배운 곡선의 길이를 구하는 공식을 활용하자.
\[l=\int_{a}^{b}\sqrt{\lbrace f'(t)\rbrace^2+\lbrace g'(t)\rbrace^2}\]여기에 $f(x,y)$를 가중치로 생각하여 곱해주면
\[\int_{C} f(x,y)\ ds=\int_{a}^{b}f(x(t),y(t))\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}\ dt\]3차원으로 확장하면 단순히 $z$축에 대한 정보를 식에 포함시켜주면 된다.
가 된다. 우리가 고등학교 때 배운 곡선의 길이는 2차원 위에서의 연산이었기 때문에 가중치를 1로 본것과 동일하다.
이해를 돕기 위해 예시 문제를 하나만 풀어보자.
\[\int_{C}(x^3+y)ds\]를 구하자. 이때,
\[x=3t, y=t^3, 0\leq t\leq 1\] \[\int_{C}(x^3+y)ds=\int_{0}^{1}(27t^3+t^3)\sqrt{3^2+(3t^2)^2}\ dt\] \[=28\int_{0}^{1}t^3\sqrt{9t^4+9}\ dt=21\int_{0}^{1}4t^3\sqrt{t^4+1}\] \[=21\int_{1}^{2}\sqrt{u}\ du=14(2\sqrt{2}-1)\]벡터장에서의 선적분
- https://angeloyeo.github.io/2020/08/17/line_integral.html
- https://mathnmath.tistory.com/100
- https://freshrimpsushi.github.io/posts/line-integral-of-vector-field/
벡터장에서의 선적분은 주어진 벡터장을 특정한 경로를 따라 지나간다고 할 때, 그 과정에서 벡터장으로부터 받는 힘의 총합을 구하는 것이다.
즉, 물리학에서 쓰이는 일의 개념과 비슷하다고 할 수 있다.
\[W=W_1+W_2+\cdots+W_n=\sum_{i=1}^{n} \overrightarrow{F_i}\ \cdot \Delta\overrightarrow{s_i}\]경로를 미세 구간 $s_i$로 잘라서 각 부분에서 한 일을 내적을 통해 구한 뒤 합해준다.
따라서 이제 미세 구간의 개수를 무한대로 보내면 다음과 같이 표현할 수 있다.
\[\int_{C} \overrightarrow{F}\ \cdot d\overrightarrow{r}\]보통 적분인자로 $s$보다 $r$을 많이 사용한다고 한다.
이해를 돕기 위해 예제 문제를 풀어보자.
벡터장이 $F=xy\hat{i}-y^2\hat{j}$로 주어져 있을 때, $y=\cfrac{1}{2}x\ (0<x<2)$ 경로를 따라 한 일의 양을 구하라.
우리가 구하려는 적분값은
\[\int_{C} \overrightarrow{F}\ \cdot d\overrightarrow{r}\]인데 여기서 $d\overrightarrow{r}$은 $x$ 방향 성분 $dx$, $y$방향 성분 $dy$의 합으로 표현할 수 있다.
\[d\overrightarrow{r}=\hat{i}dx+\hat{j}dy\]따라서 이를 식에 그대로 대입해주면
\[\overrightarrow{F}\ \cdot d\overrightarrow{r}=(xy\hat{i}-y^2\hat{j})\ \cdot \ (\hat{i}dx+\hat{j}dy)=xy(dx)-y^2(dy)\]이때, $y=\cfrac{1}{2}x$에서 $dy=\cfrac{1}{2}dx$을 대입해주면
\[\cfrac{1}{2}x^2dx-(\cfrac{1}{2}x)^2(\cfrac{1}{2}dx)=(\cfrac{1}{2}x^2-\cfrac{1}{8}x^2)dx\]따라서
\[\int_{0}^{2}\cfrac{3}{8}x^2dx=1\]선적분의 기본정리
미적분의 기본정리 2, FTC2를 선적분으로 일반화한 정리라고 볼 수 있다.
보존력이란, 어떤 힘이 한 일이 경로에 무관한 경우를 말한다. 즉, 물체에 보존력만 작용하면 역학적 에너지가 보존되고, 비보존력이 작용해 일을 하게 되면 그 일부가 열에너지 등으로 바뀐다.
예시로 보존력에는 중력, 탄성력, 전기력이 비보존력에는 마찰력등이 있다.
보존력 $F$의 특징은 퍼텐셜 에너지 $U$와 다음과 같은 관계에 있다는 것이다. $\nabla$는 기울기 연산자이다.
\[F=-\nabla U\]보존력이 한 일은 퍼텐셜에너지의 감소량과 같으므로 $W=-\Delta U$가 성립하고, 일의 정의에 의해 $dW=F\ \cdot dr$이므로
\[F=-\cfrac{dU}{dr}=-\nabla U\]면적분
앞서 평범한 1차원 적분을 확장한 것이 선적분이라면, 2차원 이중적분을 확장한 것이 면적분이다.
관련내용들
- 푸비니의 정리 : 중적분을 반복적분의 형태로 변환