이 글에서는 Exact Cover 문제들과 알고리즘 X, 그리고 최적화 테크닉 Dancing Links에 대해 다룬다.
Exact Cover
Exact Cover Problem
Exact Cover 문제의 사전적 정의는 다음과 같다.
조합론적 관점에서 보자면 주어진 집합 $X$의 부분 집합들을 원소로 가지는 집합 $S$가 주어졌을 때, $X$의 exact cover는 다음 두 조건을 만족 시키는 $S$의 부분집합 $S^*$를 말한다.
- $S^\star$는 서로소 집합이다. 즉, $S^\star$ 내부의 어떤 두 집합을 골라도, 교집합은 항상 공집합이다.
- $S^\star$의 원소들의 합집합은 $X$이다.
이는 쉽게 말해서 주어진 부분 집합들 중 서로 겹치지 않지만 전체 집합을 구성할 수 있는 조합을 찾아내는 것이다.
예시로, 집합 $X=\lbrace1, 2, 3, 4, 5, 6, 7\rbrace$와 $X$의 부분집합들의 집합 $S=\lbrace A, B, C, D, E, F\rbrace$를 잡아보자.
이때, $A=\lbrace1, 4, 7\rbrace, B=\lbrace1, 4\rbrace, C=\lbrace4, 5, 7\rbrace, D=\lbrace3, 5, 6\rbrace, E=\lbrace2, 3, 6, 7\rbrace, F=\lbrace2, 7\rbrace$ 라고 하자.
이 경우 $S$의 부분집합 $S^\star=\lbrace B, D, F\rbrace$가 $X$의 exact cover가 된다.
이처럼 포함 관계가 중심이 되는 exact cover는 다양한 형태로 표현될 수 있는데, 여기서는 추후에 설명할 알고리즘 X에서 사용될 행렬을 이용한 방법에 대해서만 알아보고자 한다.
$S$의 원소들에 대해 행을 구성하고, $X$의 원소들에 대해 열을 구성한다. 이후 $S$의 원소가 $X$의 원소를 포함하고 있으면 1, 아니면 0으로 표시한다. 위의 예시의 경우 다음과 같이 만들어진다.
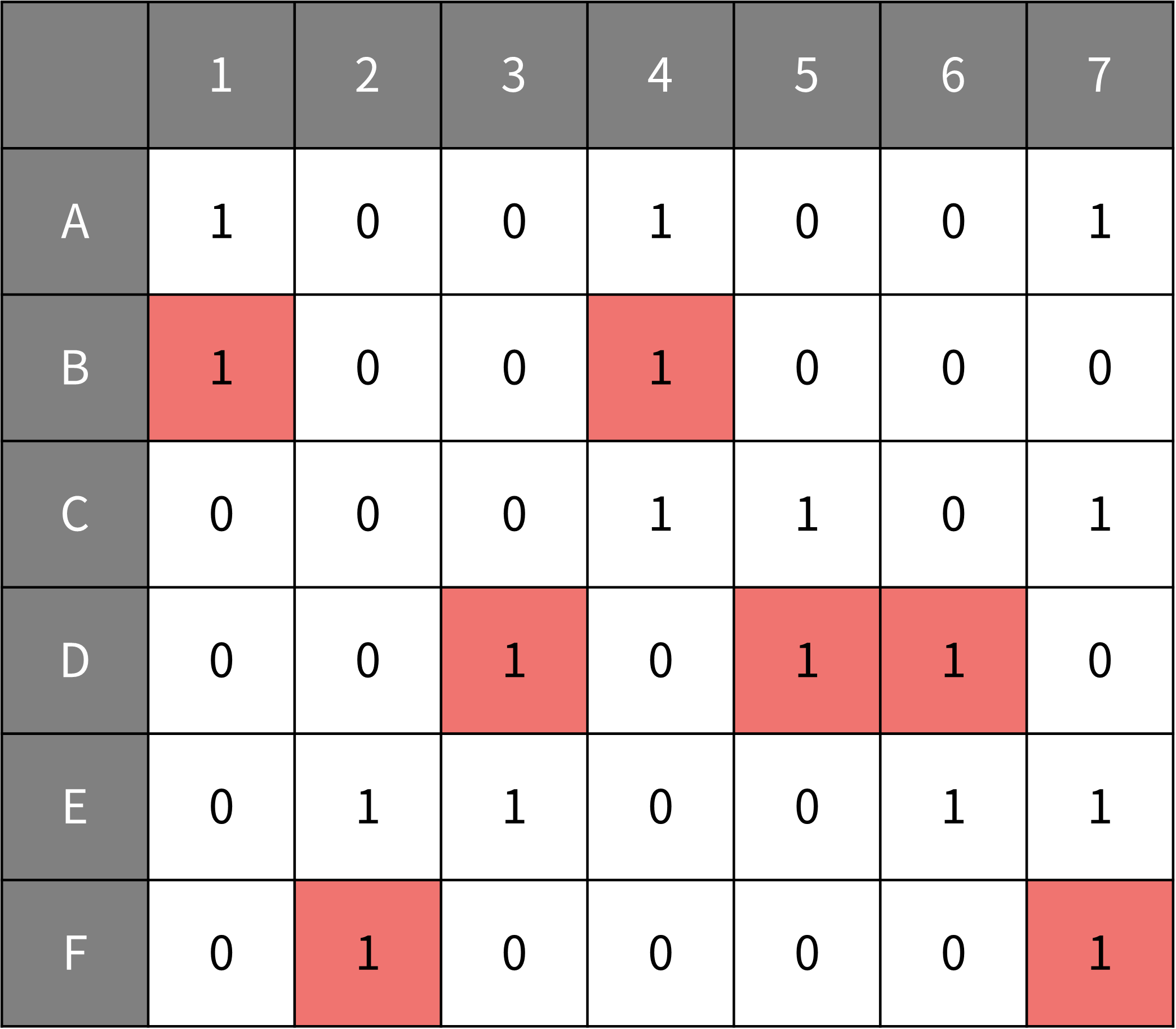
Exact Hitting Set Problem
Exact cover 문제가 부분집합의 조합을 고르는 것이었다면 이와 비슷하면서도 조금 다른 Exact Hitting Set 문제는 주어진 모든 부분집합에 대해 원소가 한번씩만 등장하는 주어진 전체집합의 부분집합을 고르는 문제이다. 이는 예시를 통해 쉽게 이해할 수 있다. 위에서 설명한 $X=\lbrace1, 2, 3, 4, 5, 6, 7\rbrace$와 $S=\lbrace A, B, C, D, E, F\rbrace$에서 Exact Hitting Set은 $X$의 부분집합 $X^\star=\lbrace1, 2, 5\rbrace$가 된다. $S$의 원소들 $A \cdots F$에 대해 $X^\star$와 겹치는 원소는 항상 1개이기 때문이다.
활용
또한 이들은 펜토미노 채우기, 스도쿠, N-Queen과 같은 문제들에 다양하게 활용될 수 있다.
펜토미노의 경우 주어진 보드의 보드칸에 그 칸의 행과 열 번호가 하나의 쌍을 이루어 적혀있다고 보고, 펜토미노를 임의로 보드에 놓았을 때 차지하는 칸에 적힌 숫자를 하나의 집합으로 볼 수 있다.

위와 같이 중심이 뚤린 판을 채우는 경우 다음과 같이 집합을 만들 수 있다.
- $\lbrace F,12,13,21,22,32\rbrace$
- $\cdots$
- $\lbrace L,12,22,32,42,43\rbrace$
- $\cdots$
스도쿠의 경우 이보다는 조금 더 복잡하다. 일반적인 $9\times 9$ 스도쿠는 4가지 조건들을 만족시켰을 때 스도쿠를 해결했다고 정의된다.
- 한 칸에는 오직 한 숫자만 존재한다
- 각 행에 중복된 숫자가 존재하지 않는다.
- 각 열에 중복된 숫자가 존재하지 않는다.
- 각 $3\times 3$ 칸 안에 중복된 숫자가 존재하지 않는다.
자, 그러면 보드에서 $(x,y)$ 칸에 위치한 숫자를 $z$라고 정의하자.
\[RxCy\#z\]그러면 위와 같이 $9\times 9\times 9=729$개의 경우의 수를 표현 할 수 있다. 그리고 이들을 앞서 설명한 행렬에서 행에 위치 시키고 앞서 말한 조건들을 열에 위치 시킬 수 있다.
이때 조건들은 다음과 같이 표현할 수 있다.
- $RxCy$ : $(x,y)$ 칸에 위치할 수 있는 숫자
- \(Rx\#z\) : $x$ 번째 행에 오는 숫자 $z$
- \(Cy\#z\) : $y$ 번재 열에 오는 숫자 $z$
- \(Bk\#z\) : $k$ 번째 상자에 들어가는 숫자 $z$
이후 조건에 포함되는 수들은 1로 표현해주면 다음과 같이 $729\times 324$ 크기의 행렬이 만들어진다.
\[\begin{matrix} &R1C1&R1C2&\cdots&R1\#2&R1\#2&\cdots&C1\#1&C1\#2&\cdots&B1\#1&\cdots\\ R1C1\#1&1&0&\cdots&1&0&\cdots&1&0&\cdots&1&\cdots\\ R1C1\#2&1&0&\cdots&0&1&\cdots&0&1&\cdots&0&\cdots\\ \vdots\\ R1C2\#1&0&1&\cdots&1&0&\cdots&0&0&\cdots&1&\cdots\\ \vdots\\ R9C9\#9&0&0&\cdots&0&0&\cdots&0&0&\cdots&0&\cdots \end{matrix}\]크누스의 알고리즘 X - Knuth’s Algorithm X
정의
크누스의 알고리즘 X는 앞서 설명한 exact cover 문제를 푸는, 즉 행렬에서 각 열에 1이 한번씩만 등장하도록 적절한 개수의 행을 고르는 행위를 목표로 하는 알고리즘이다.
과정
만약 주어진 행렬 $A$에서 남은 열이 없고, 현재 구한 해가 옳다면 종료
1. 열 하나를 고르고 이름을 $c$라 정의한다.
2. $A_{r,c}=1$인 행 $r$을 고른다.
3. 행 $r$을 부분해에 포함시킨다.
4. $A_{r,j}=1$을 만족시키는 모든 열 $j$에 대해서 $A_{i,j}=1$을 만족시키는 행 $i$를 행렬에서 제거하고 이후 열 $j$도 행렬에서 제거한다.
5. 재귀적으로 반복해준다.
이때, 1번째 과정에서는 특정 규칙에 기반, 즉 결정론적으로 열을 고르고, 2번째 과정에서는 비결정론적으로 행을 고른다.
여기서 비결정론적으로 고른다는 의미는 임의로 선택하여 부분 알고리즘으로 분할한다는 것이다. 쉽게 말해서 탐색을 한단계 더 들어가서 진행한다는 것이다.
춤추는 링크 - Dancing Link
이 부분은 이중 연결 리스트에 대한 기초적인 개념이 필요하다. 여기를 참고하자.
정의
알고리즘 X의 효율적인 구현에 사용되는 테크닉이다. 이 테크닉의 핵심 아이디어는 이중 연결 리스트의 원소 삽입과 삭제 과정에서 발견되었다고 한다.
1
2
3
4
5
6
//삽입
x.left.right ← x;
x.right.left ← x;
//삭제
x.left.right ← x.right;
x.right.left ← x.left;
알고리즘 X에서 가장 핵심이 되는 부분은 $1$을 찾는것인데, 항상 전체 탐색을 하기에는 시간이 너무 많이 소비된다는 단점이 있다. 하지만 만약 값이 $1$인 부분만 들어내서 서로 연결시켜주면 어떨까? 좌우로는 같은 행에서 1인 값들끼리, 상하로는 같은 열에서 1인 값들기리 연결을 해주는 것이다!
또한 각 열에 대해서는 열의 이름과 그 열에 속한 노드의 개수를 저장하고 있는 List Header 노드와 이들을 관리하는 Header 노드를 추가해준다.
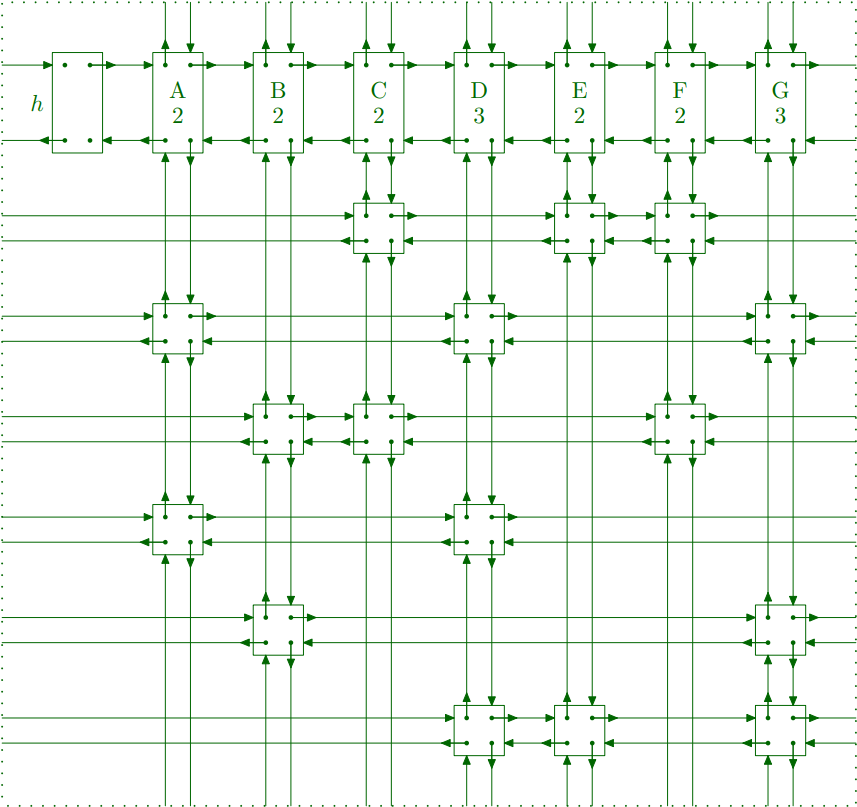
자, 이로써 준비는 끝났다! 본격적으로 알고리즘에 대해 알아보자.
과정
알고리즘의 진행 과정은 앞서 설명한 내용과 별반 다르지 않다.
먼저 알고리즘의 종료 조건인 더 이상 열이 남지 않았을 때는 Header 노드가 자기자신으로 다시 연결되어있는지 확인해주면 된다.
아직 탐색이 더 가능하다면 특정한 규칙(보통 1의 개수가 가장 작은 열을 찾는다)에 따라 열을 고르고, cover 를 해준다. 여기서 cover 란 행에 속해있는 각 원소들이 포함된 열에 속한 원소들을 위 아래로 끊어주는 것이다. 이후 끊어진 원소들에 대해서도 다시 cover 를 진행해준다.
이로써 한단계가 끝났다. 이후 재귀적으로 더 깊게 탐색을 시행해주고, 만약 탐색을 실패했다면 uncover 를 진행해주면 된다. 여기서 탐색의 실패란 고른 열에서 $1$이 더 이상 없는 경우를 뜻한다.
구현
그러면 이제 구현을 해 볼 차례이다!
먼저 행렬이 주어졌을 때 연결 리스트를 만들어보자.
일단 연결 리스트에 사용될 노드를 다음과 같이 정의할 수 있다.
1
2
3
4
5
6
7
8
9
10
struct node
{
int row;
int size;
node* column;
node* up;
node* down;
node* left;
node* right;
};
행렬이 주어졌을 때 먼저 각 열에 대해서 header 를 먼저 관리해 주자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void solve(vector<vector<int>>&mtx)
{
int n = mtx[0].size();
vector<node> col(n);
node header;
header.right = &col[0];
header.left = &col[n-1];
for(int i=0;i<n;++i)
{
col[i].size = 0;
col[i].up = col[i].down = &col[i];
col[i].left = i?&col[i-1]:&header; //왼쪽 끝인지 판별
col[i].right = i==n-1?&header:&col[i+1]; //오른쪽 끝인지 판별
}
}
이후 값이 1인 경우에만 서로 연결 시켜주면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
for(int i=0;i<mtx.size();++i)
{
node* last = nullptr
for(int j=0;j<n;++j)
{
if(mtx[i][j])
{
node* now = new node;
now->row = i;
now->column = &col[j];
now->up = col[j].up;
now->down = &col[j];
if(last) now->left=last,now->right=last->right,last->right->left=now,last->right=now;
else now->left=now,now->right=now;
col[j].up->down=now;
col[j].up=now;
col[j].size++;
last = now;
}
}
}
탐색 함수는 위에 설명했던 내용들을 그대로 구현하면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
bool search(node* header)
{
//성공
if(header->right==header) return 1;
//특정한 규칙(1의 개수가 가장 작은 열; 이 부분은 논문을 참고하자)
node* col=nullptr; int low = ~(1<<31);
for(node* it=header->right;it!=header;it=it->right)
if(it->size < low)
{
if(it->size==0) return 0;
low = it->size;
col = it;
}
//선택한 열 cover
cover(col);
for(node* it=col->down;it!=col;it=it->down)
{
for(node* jt=it->right;jt!=it;jt=jt->right) cover(jt->column);
if(search(header))
{
//정답 찾음
//row가 정답이 되고, 배열에 넣어서 리턴하거나
//지금처럼 데이터에서 바로 추출해서 값을 저장해줘도 된다.
sdk[v[it->row].row][v[it->row].col]=v[it->row].val;
return 1;
}
for(node* jt=it->left;jt!=it;jt=jt->left) uncover(jt->column);
}
uncover(col);
return 0;
}
cover 함수와 uncover 함수 또한 시작 노드에서 한 바퀴 순회하면서 링크를 끊어주면 된다. 이때 uncover 함수는 cover 함수에서 끊었던 순서를 거꾸로 따라가 줘야 오류가 나지 않는다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void cover(node* c)
{
c->right->left = c->left;
c->left->right = c->right;
for(node* it=c->down;it!=c;it=it->down)
for(node *jt=it->right;jt!=it;jt=jt->right)
{
jt->down->up = jt->up;
jt->up->down = jt->down;
jt->column->size--;
}
}
void uncover(node* c)
{
for(node* it=c->up;it!=c;it=it->up)
for(node* jt=it->left;jt!=it;jt=jt->left)
{
jt->down->up = jt;
jt->up->down = jt;
jt->column->size++;
}
c->right->left = c;
c->left->right = c;
}
이로써 핵심 함수들을 구현하였고, matrix를 설계하는 부분은 인덱스만 조금 고려해서 넣어주면 별 문제 없이 문제를 해결할 수 있다.
참고문헌
- https://en.wikipedia.org/wiki/Exact_cover
- https://en.wikipedia.org/wiki/Knuth%27s_Algorithm_X
- https://en.wikipedia.org/wiki/Dancing_Links
- https://www.geeksforgeeks.org/introduction-to-exact-cover-problem-and-algorithm-x/
- https://infossm.github.io/blog/2019/12/15/knuths-algorithm-x/
- https://jeonggyun.tistory.com/225